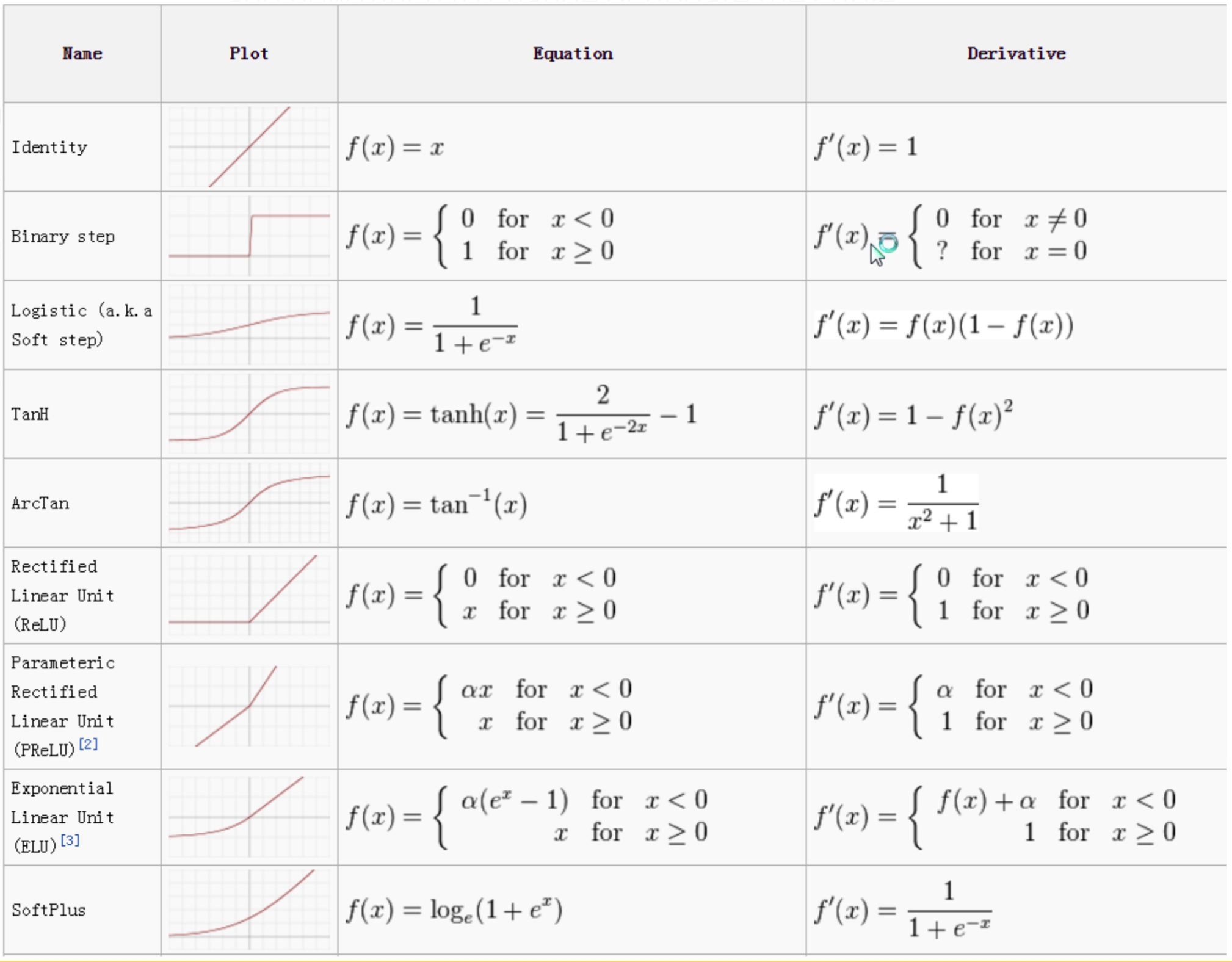
Today we will look at different activation functions, especially the family of ReLU (Rectified Linear Unit) activation function. The role of activation functions in neural networks is taking the input and mapping it into output that goes into next layer. Deciding which activation function to use heavily depends on the target. Overall, there are two types of activation functions :
Linear and Non-linear activation functions
though non-linear functions are mostly used. The simplest of linear activation functions takes the form $ f(x) = x$. Therefore, the output of the functions will not be confined between any range. Usually, neural networks are used to predict scores that are bounded by a certain range, so linear activation function is not common. Other important things to consider in activation functions are whether they are differentiable or monotonic.
Differentiable and monotonic activation functions
In neural networks, most activation functions are differentiable. This feature is important because weights and biases are updated via back propagation, where gradients are used. If the gradients approach 0, the model would not learn anything. Activation functions have to be also monotonic. This answer from StackExchange by Kyle Jones perfectly explains the reason.
“During the training phase, backpropagation informs each neuron how much it should influence each neuron in the next layer. If the activation function isn’t monotonic then increasing the neuron’s weight might cause it to have less influence, the opposite of what was intended. The result would be choatic behavior during training, with the network unlikely to converge to a state that yields an accurate classifier. “
Now you may have one question : Many activation functions (like ReLU that we will cover today) are not differentiable at all points. What about them? –> The answer is that although it is not mathematically undoubtful, functions are not evaluated at those points and instead, return reasonable values such as 0 or 1. For ReLU, the function returns 1 for $x>=1$.
Now let’s look at different types of non-linear activation functions. The most common non-linear activation funcitons are :
Sigmoid, Hyperbolic-tangent activation function, ReLU
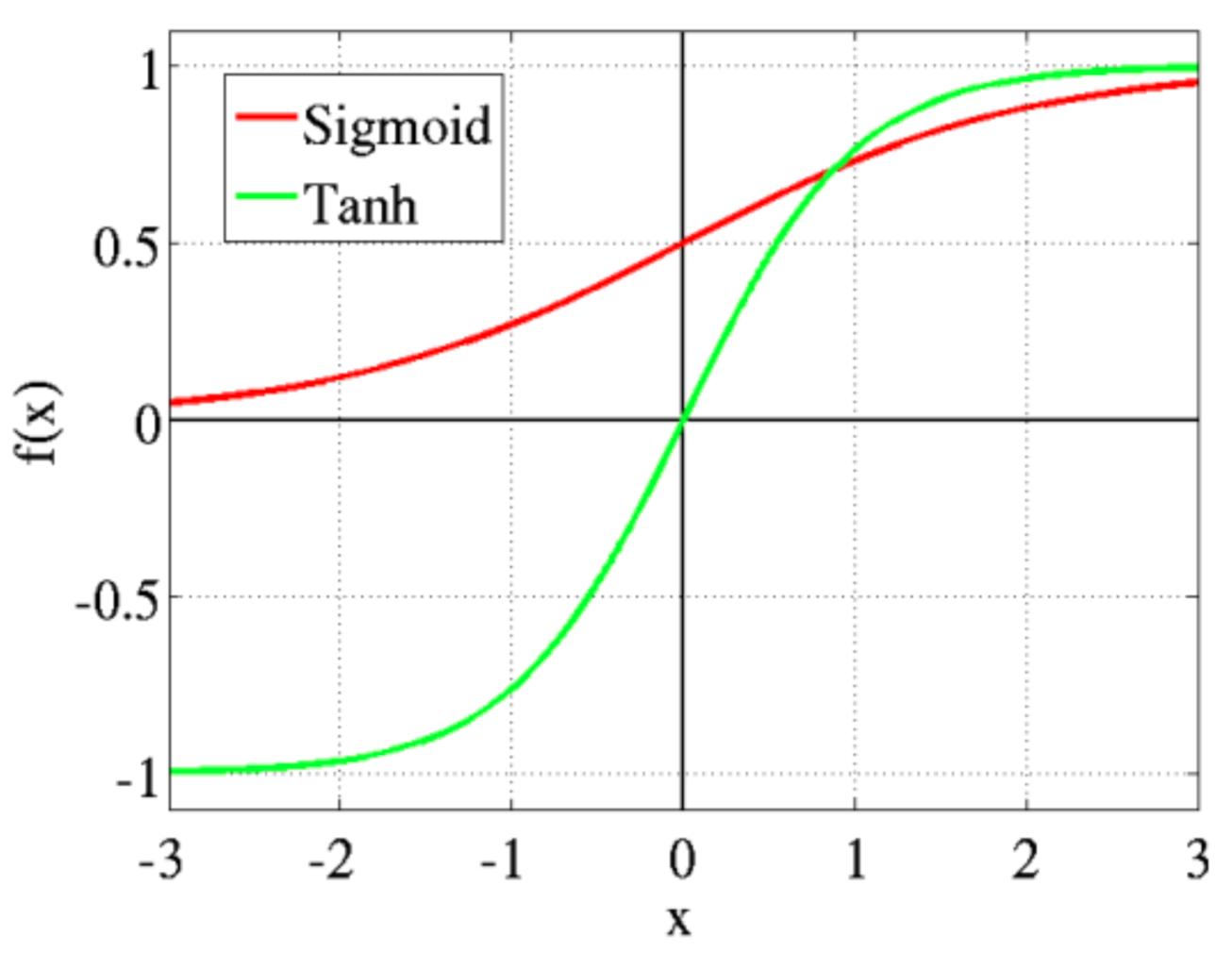
Sigmoid / Hyperbolic-tangent
\[\frac{1}{1+e^{-x}}\]Because the range is confined to be between 0 and 1, it is often used in predicting probability tasks.
\[\frac{e^{2x}-1}{e^{2x}+1}\]Shape of tanh is similar to sigmoid. The only difference is that tanh is symmetric around zero. Advantage is that the negative values will strongly be mapped negative and zero near zero. It is used in two-class classification task. When classifying multiple classes, we use Softmax function.
ReLU
\(relu(x) = max(1,x)\)
ReLU aims to resolve vanishing or exploding gradients problem that arises when the model gets deeper. The activation functions’s gradient is confined to 0~1. Bur ReLU still has some problems. Because gradient is 0 at some nodes, those nodes will not contribute to network anymore. This is called dying ReLU.
Leaky ReLU (LReLU)
\(lrelu(x)= \begin{cases} &\alpha x \text{ if }x\leq 0\\ &x \text{ if } x> 0\\ \end{cases}\)
where $\alpha = 0.01$. (If $\alpha$ is trainable, it becomes paramterized ReLU) Because the gradient is a very small number $\alpha$ instead of 0 (the leak),
Exponential Linear Unit (ELU)
\[\elu(x)= \begin{cases} &\alpha(exp(x)-1) \text{ if }x\leq 0\\ &x \text{ if } x> 0\\ \end{cases}\]where $\alpha=1$ ELU speeds up learning by centering activations around zero, rather than using batch normalization. It decreases the bias (the ouput is always positive or 0) shift present in ReLU that slows down learning.
Scaled Exponential Linear Unit (SELU)
\(selu(x)= \lambda \begin{cases} &\alpha(exp(x)-1) \text{ if }x\leq 0\\ &x \text{ if } x> 0\\ \end{cases}\)
where $\alpha = 1.6733, \lambda = 1.0507$. It is scaled version of ELU and thus has unit variance. As layers are increased, activations will converge to zero mean and unit variance and make learning highly robust.
In this paper, the author tests the perforrmances of these activation functions on MNIST data with different learning rates. SELU and ELU performed the best.
Swish
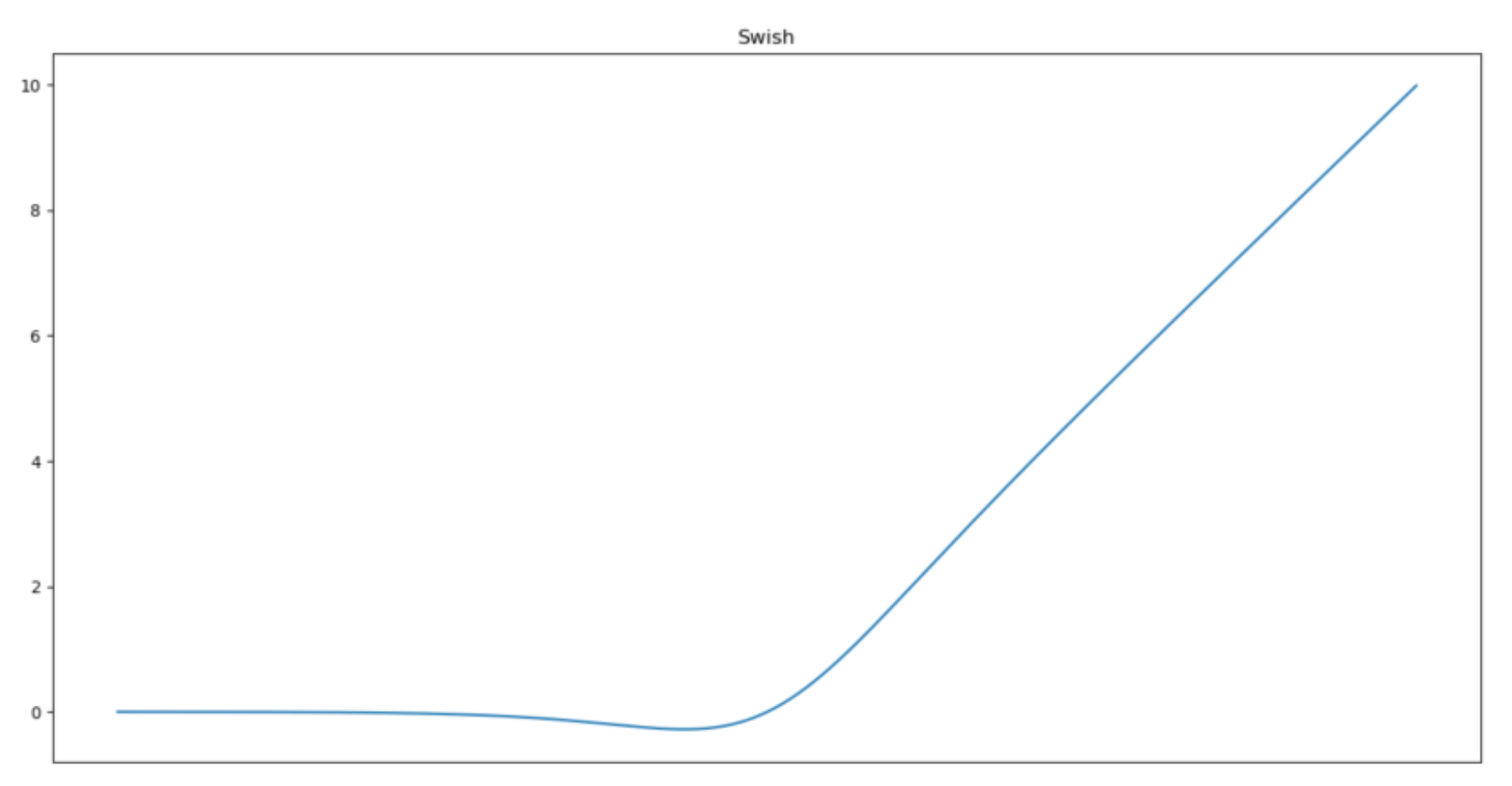
This activation function was developed by Google engineers. It performs fast and more accurately when model gets deeper. The function is differentiable at all points but is not monotonic. This means that activations may decrease even when inputs are increasing.
Overview