Sparse Transformer
Do you remember the fact that there is a restriction on the max length of input tokens in BERT package? More than 512 tokens per sentence/input are not allowed to be used as an input. This is one of the disadvantages that BERT has - the more tokens we have, the more exponential the computation. In other words, existing Transformer models have the problem of increasing memory and computational needs as the sequence length increases.
To alleviate this problem, OpenAI presented the paper named “Generating Long Sequences with Sparse Transformers“(2019). The paper complements this by presenting a methodology that can reduce unnecessary computation and reduce memory usage through compression or recomputation, and further reconstruct residual block and weight initialization to significantly improve Transformer training for very deep networks in conclusion. (Note - Traditional: O(n^2d) -> Sparse Trans: O(n*sqrt(n)))
In this posting, I will focus on the core part of this paper (= Factorized self-attention) and briefly mention rest of the stuffs.
Motivation
The paper team first studied in what pattern Transformer’s attention technique is being learned. Let’s look at the figures below.

In the process of 128 layers of traditional transformer learning CIFAR-10 datasets, the pixels are brightly represented to determine where the most attention-seeking pixels are when generating the next pixel. First, if you look at (a), early layers of the network first explore locally connected patrons. (b) shows that layers 19-20 split attention into row & column attention. (c) indicates that some attention layers show global & data-dependent access patterns. Finally, (d) indicates that the latter 64th to 128th layers are only focused on the speci£c input patters, showing high sparsity.
The paper team noted that such a traditional Transformer exhibits a certain pattern in learning something, i.e., it gives attention to only a small amount of sparse data in the end. So they came up with the idea - why don’t we just learn sparsely from the beginning?
Factorized Self-attention
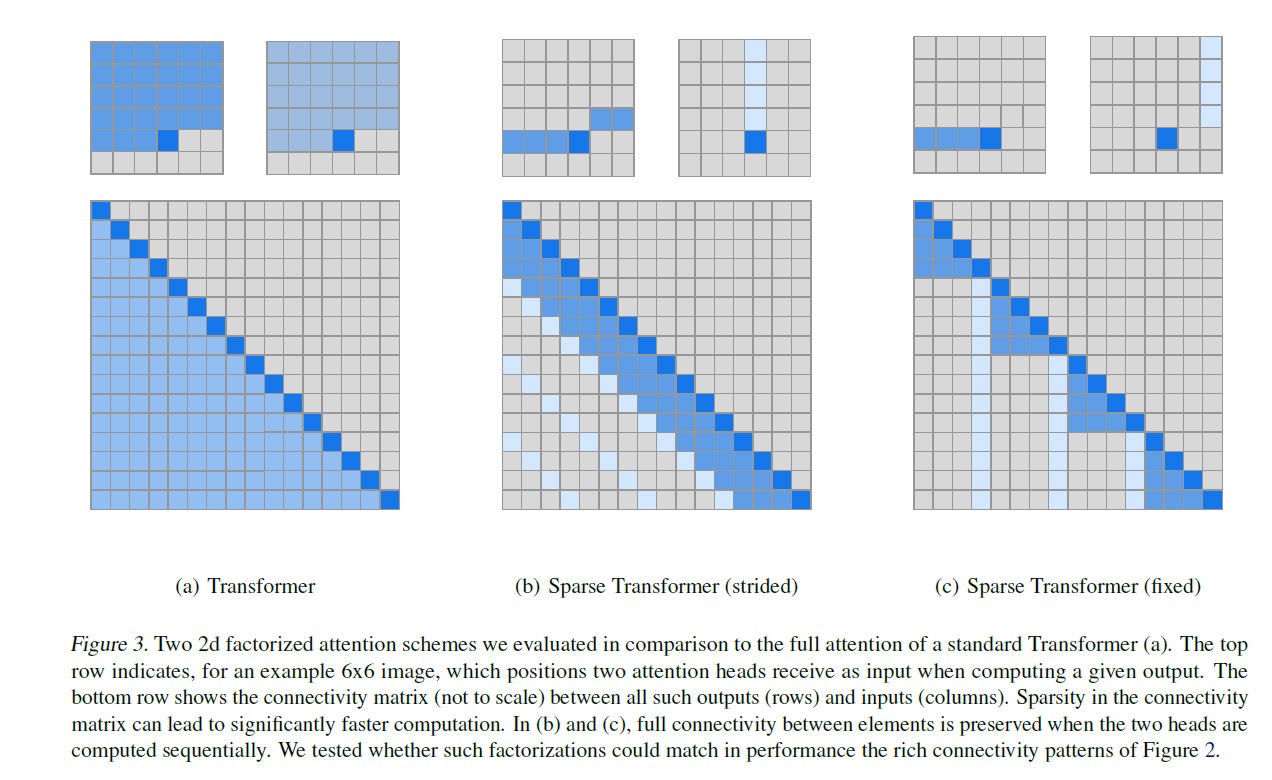
The Full Self-attention covered in the last posting calculates the attention for all previous values, as shown in (a). However, in Factorized Self-attention, the method gives attention to only a fraction of the previous value, not all, and it just varies slightly depending on whether it is Strided or Fixed.
Strided attention (Figure (b)) is to have one head attend to the previous l locations and the other head attend to every l th location, where l is the stride and chosen to be close to sqrt(n). The formula is as follows :
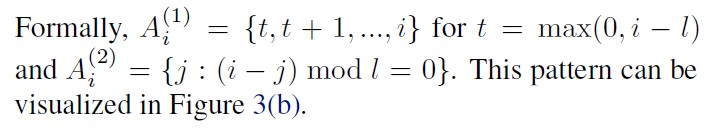
This formulation is convenient if the data naturally has a structure that aligns with the stride, like images or some types of music. However, for data without a periodic structure like text, the paper team found that the network can fail to properly route information with the strided pattern, as spatial coordinates for an element do not necessarily correlate with the positions where the element may be most relevant in the future.
In those cases, it is useful to use Fixed attention (Figure (c)) pattern, where specific cells summarize previous locations and propagate that information to all future cells. The detailed formula of fixed attention is shown below :
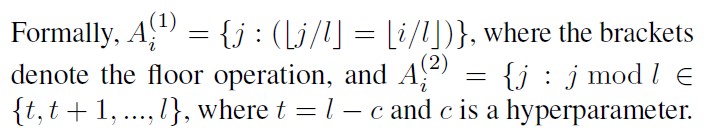
-> EX) If the stride is 128 and c=8, all future positions greater than 128 can attend to positions 120-128, all positions greater than 256 can attend to 248-256, and so forth.
Thus, using FACTORIZED Self-attention instead of FULL Self-attention can alleviate the problem of computing long sequence data with Traditional Transformer.
The above concept of Factorized Self-attention is one of the main parts of the paper, so from now on, I will briefly mention about rest of the contents.
Factorized attention heads
There are 3 techniques for integrating factorized self-attention.
-
Use one attention type per residual block and interleave them sequentially or at a ratio determined as a hyperparameter.
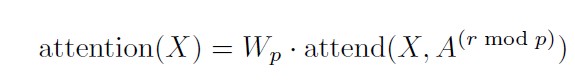
-
Have a single head attend to the locations of the pixels that both factorized heads would attend to, which we call a merged head.
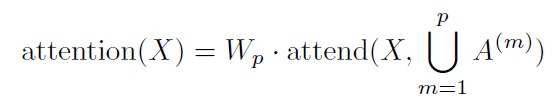
-
Use multi-head attention, where n_h attention products are computed in parallel, then concatenated along the feature dimension.
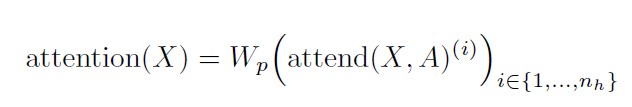
** Here, A can be the separate attention patterns, the merged patterns, or interleaved as in Full Self-attention heads.
The dimensions of the weight matrices inside the attend function are reduced by a factor of 1/n_h, such that the number of parameters are invariant across values of n_h.
Saving memory by Recomputation
The paper said that we can save much memory via Gradient Checkpointing. It has been shown to be effective in reducing the memory requirements of training deep neural networks. However, this technique is particularly effective for self-attention layers when long sequences are processed, as memory usage is high for these layers relative to the cost of computing them.
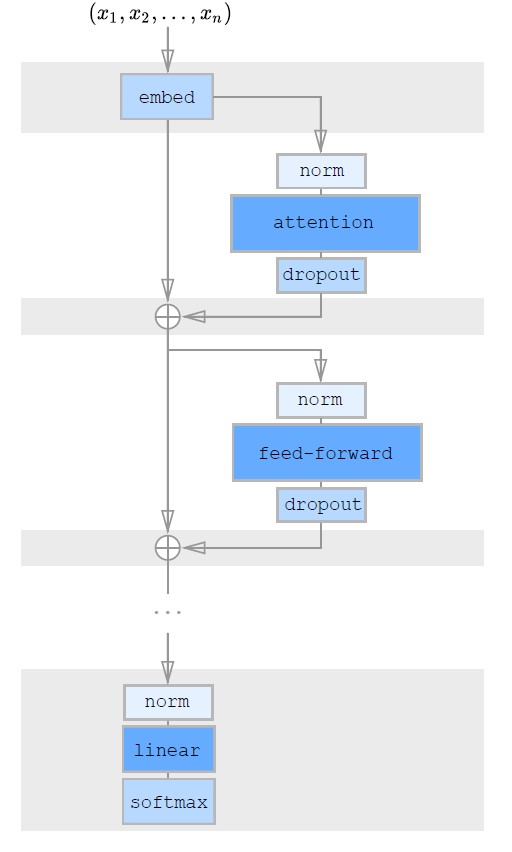
The shaded background indicates tensors which are check-pointed and stored in GPU memory. The other tensors, including the attention weights and feedforward network activations, are recomputed during the calculation of gradients, reducing memory usage substantially.
Conclusion
So far, we have summarized the overall contents of the Sparse Transformer paper. I hope it will be helpful for those who want to study this topic because I tried to explain it using intuitive pictures rather than formulas to help them understand it more easily. I highly recommend for those who want to learn about Reconstruction of Residential Block & Weight Initialization, which was not covered in this posting, to read OpenAI’s paper. In the next NLP posting, I will talk about Big Bird, an NLP model using Sparse Transformer.
Reference :
- https://arxiv.org/pdf/1904.10509.pdf
- https://judy-son.tistory.com/5
- https://github.com/YoonjinXD/Yoonjin/blob/master/posts/Transformer.md
